Why you might fold J6s in the small blind
I was recently involved in a discussion with some poker buddies about a hand where the hero had jack-six-suited in the small blind of a $1/2 no-limit hold’em game. There were two limps but no raise in front of him, he tossed in the missing dollar and the big blind checked. He flopped a full house; that’s where things got interesting.
In responding, I started with, “Well, I’d fold the J6s in the first place, but as played…”
Everybody immediately came back and said (in one way or another), “Don’t be ridiculous - of course you call for the extra dollar; you’re getting 7:1 pot odds.”
Here’s my longer form reply.
First, almost as an aside, it’s not “a dollar”. It’s one half of a big blind. That is, would your answer be any different if we were playing $50-100 NLHE and it cost $50 to complete the big blind? If so, then our perspectives on the game are very different.
Anyway… Yes, you’re getting 7:1 odds. But so what? 7:1 odds is only useful information in the context of your chances of acquiring that reward. That is, if I said to you, “Hey, I’m getting 7:1 odds in this pot - should I call?” You’d probably say, “I need to know more information to answer that question.” Well, this is exactly that situation.
7:1 seems like a big number (unless you grew up playing limit hold’em; then it seems like a perfectly normal number). But is it big enough to justify calling with a crap hand in the worst position in all of poker? People often say, “It’s a cheap ticket to the flop lottery; what if my numbers hit?” But there’s a problem with that analogy. In a lottery, your numbers hit or they don’t. If they hit, you go collect your winnings and all is well. If they don’t, you tear up your lottery ticket and get on with your life. [1]
If your J6s flops a full house, then fine, you’ve hit the lottery - collect as much as you can. But that’s not how J6s usually flops equity. And the problem is realizing that equity. For instance, what is the most likely way that J6s will have some decent value postflop?
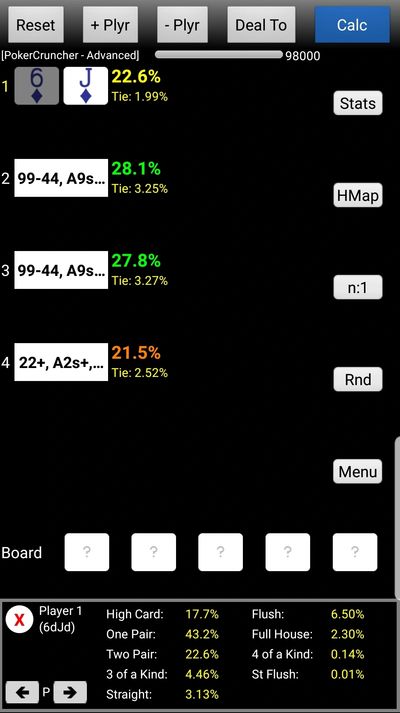
Rather than wave my hands at the problem, I asked PokerCruncher how J6s is doing against three other hands: two hands that are the top 40% of hands, less the top 9% (on the assumption that they’d raise their top 9%) and one random hand (the big blind, who checked). Well, it’s got 22.6% equity, which is barely better than the 21.5% equity that BB’s random hand has (it ties for at least some of the pot 2% of the time). 43% of the time, it will finish the hand with one pair - it’s pretty clear that this where this hand gets its most equity - from a board where a pair of jacks is best.
So you have Jd6d, and complete the blind. Big blind checks and the flop comes Jh-9c-2d.
Now what? I mean, this is a “good” result by the standards of J6s. It’s quite possible, perhaps probable, that you have the best hand. Do you bet it into three opponents? Do you check and call a bet? You do have top pair and three to a flush (though this is starting to get expensive). Name a turn card that you love (I can think of five, though if there’s another jack out there and you make trips, you’re probably about to get stacked).
In fact, if you have the best hand, you’re unlikely to get much value for it. Nobody with a worse hand will call much, and if anybody puts pressure on you, you just can’t continue. Suppose you bet out on the flop and get raised. Well, that’s a better jack, or QT, or T8. Care to spend two and half more out-of-position streets to find out which it is? Same problem if you check and the last guy bets. Positional bet with air? Better jack? Good draw?
Another place you pick up equity is by flopping a flush draw. The flop comes Kd-Ts-3d. Whee, you’re only 2:1 dog to get a flush by the river, which will almost certainly be the best hand. But to get to the river, you need to cross two streets. And with that flop, you’ll have to weather serious betting on the way, again, out of position. That betting will either deny you your chance to see the river card, or force you to pay more than the odds justify (which destroys your preflop lottery argument).
Here’s one way to look at it: suppose that half a blind you’re calling preflop represents the only chips left in front of you (it’s easy to imagine a tournament situation where this happens). Then I’d say 7:1 is a fine price. You’re all-in and, if you believe my calculations, your J6s is just a hair worse than 3:1 underdog to two hands that limped and a random hand in the big blind. Crucially, you get to see all five cards. You sit back and see if your lottery numbers come up.
Also, I will quickly grant that there is some price for which you’d be crazy not to call half a blind in the small blind with J6s. Suppose that just before I acted, the poker room manager walked by, said “Splash pot!” and dropped 100 blinds worth of chips into the pot. I’d immediately throw in my half a blind and take my chances with subsequent action.
But neither of those above scenarios are common. In the real world, you toss in that half a blind and then all the rest of your chips are at stake as you try to realize your hand’s equity.
People who know me know that I’m a tight player. I like playing big hands in position. I like flopping sets and check-raising the guy who flopped top pair but is drawing near-dead. I take no joy in navigating two or three streets of betting with a painfully marginal hand, out of position, just because I flopped enough that I feel obliged to continue.
So I just fold J6s in the small blind, even for half a blind. If you choose to complete, I certainly wish you success.
-------
[1] I need to note that this “false lottery analogy” idea originally came from Tommy Angelo. That said, any misrepresentation of his original theory is my fault, not his.
-------
“No one loves poker more than Lee Jones,” says Jason Somerville, along with everyone who knows Lee. And now Lee Jones is sharing his accumulated wisdom and poker expertise by way of customized coaching. Click here to set up your first session.